بحث الفيزياء

الحركة الدورانية

أو حركة الاستدارة هي حركة التفاف حول مركز الجسم نفسه، بخلاف الحركة الدائرية التي يحافظ فيها الجسم على مسافة ثابتة من مركز يقع خارجه.

كرة تدور حول أحد أقطارها، في نقطة ثابتة.
وتكون الحركة دورانية منتظمة إذا كانت سرعة الدوران ثابتة، وإلا يقال عن تلك الحركة الدورانية أنها غير منتظمة لتغير سرعة الدوران.

وعزم القوة هو الذي يسبب الحركة الدورانية.

لا يمكننا الحديث عن الحركة الدورانية لشيء إلا إذا أهملنا حجمه، ويتم اعتبار هذا الشيء جسما نقطيا.

أمثلة
1حركة مركز المروحة دورانية، أما أذرعها فحركتها دائرية
2دوران الأرض حول نفسها
3دوران الافعوانية حول نفسها
4دوران العجلة حول نفسها
٭5دوران النواعير بفعل المياه الجارية

إزاحة زاوية
إضافة وصف المقالة
المراد بإزاحة الجسم المادي إزاحة زاوية إدارته حول محور ثابت بزاوية معينة. ربما سميت زاوية الإزاحة بنفسها الإزاحة الزاوية تسمية بالمصدر.

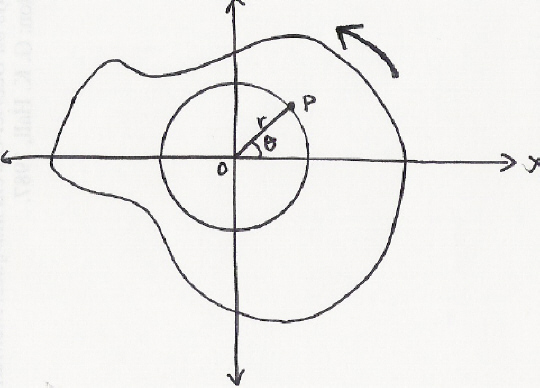
زاوية الإزاحة (θ

بالراديان) هي نسبة قوس الإزاحة إلى الشعاع. θ = s / r
يعتبر اتجاه الدوران في عكس اتجاه عقارب الساعة موجبا، ويعد سالبا إذا كان في اتجاه حركة عقارب الساعة

سرعة متجهة
معدل تغيير موضع كائن كدالة للوقت ، واتجاه هذا التغيير
هي المسافة التي يقطعها الجسم في وحدة الزمن وهي قيمة متجهة، أي تتميز باتجاه معين. هذه خاصية هامة للسرعة. أولا السرعة لها قيمة معينة تقاس المتر/ثانية أو كيلومتر/ساعة، وثانيا نميز اتجاه السرعة في الرياضيات بسهم لتسهيل الحسابات.

أنواع السرعة المتجهة

السرعة a والسرعة المساوية في عكس الاتجاه -a، وضعف السرعة 2a وفي نفس اتجاهها.
تمثل السرعات المتجهة بأسهم تتناسب أطوالها مع مقدار السرعة، ويتخذ اتجاه السهم اتجاه السرعة. انظر الشكل : السرعة a والسرعة المساوية في عكس الاتجاه -a، وضعف السرعة 2a وفي نفس اتجاه السرعة a.

هناك نوعين من السرعة:

سرعة خطية = المسافة/الزمن وحدتها (متر/الثانية)أو(ميل/الثانية).
سرعة زاوية أو سرعة دورانية: عدد دورات/الزمن وحدتها (دورة/ثا).
وتختلف طريقة قياس الوحدة المستخدمة في الزمن طبقا للنظامين العالمي (المتري) والإنجليزي. فمثلا في دولة المغرب مقياس السرعة هو بالكيلومتر لكل ساعة (نظام الوحدات الدولي) أما في الولايات المتحدة الأمريكية فهي بالميل لكل ساعة (النظام الإنجليزي). ويجب معرفة الفرق بين الميل والكيلومتر لمعرفة كيفية المقارنة بين السرعتين.

فمثلاً، قطعت سيارة مسافة 100 كيلو متر خلال 30 دقيقة، وسرعة السيارة = المسافة بالكيلومتر/الزمن بالساعات سرعة السيارة = 100 / 0.5، إذاً سرعة السيارة هي 200 كيلومتر لكل ساعة.

السرعة المتوسطة
 
السرعة المتوسطة فهي المسافة الكلية التي يجتازها جسم مقسومة على مدة اجتيازه هذه المسافة ووحدتها متر /ثانية.

التسارع
والسرعة غير العجلة أو التسارع حيث التسارع هو كل تغيّر في مقدار السرعة أو في اتجاهها خلال وحدة زمنية.
وحدة العجلة: (متر/ثانية) /ثانية أي متر في الثانية المربعة، أو (كيلومتر/ساعة)/ساعة أي كيلومتر في الساعة المربعة

سرعة زاوية
إضافة وصف المقالة
في الفيزياء، السرعة الزاوية هي متجهة التي تعبر عن التردد الزاوي والمحور الذي يدور حوله الجسم. وحدة قياس السرعة الزاوية في نظام الوحدات الدولي هي الراديان/ثانية ، ومن الممكن قياسها بواحدات أخرى مثل درجة في الثانية. عندما تُقاس بوحدة دورة في وحدة الزمن (دورة في الدقيقة، أو دورة في الساعة…الخ) فإنه يطلق عليها اسم السرعة الدورانية.

السرعة الزاوية تعبر عن سرعة دوران وجهة الدوران حول المحور
يُرمز للسرعة الزاوية بالحرف أوميغا (Ω أو ω). جهة متجهة السرعة الزاوية تكون عمودية على مستوي الدوران، والتي تـُحدد غالباً باستخدام قاعدة اليد اليمنى.

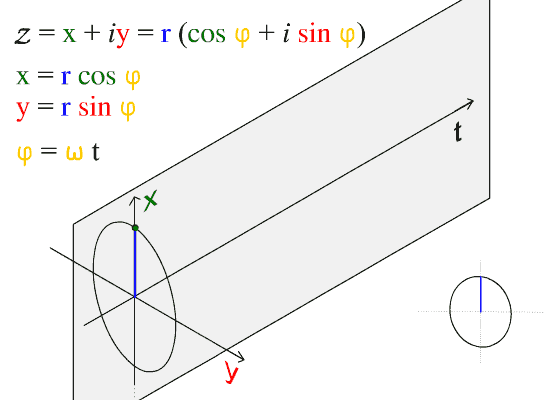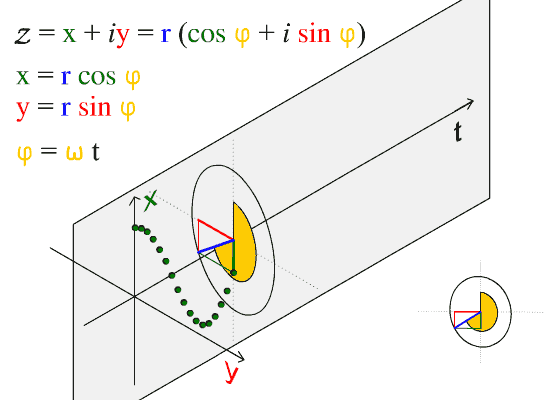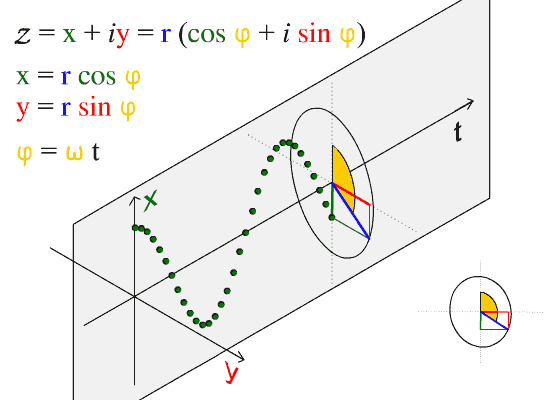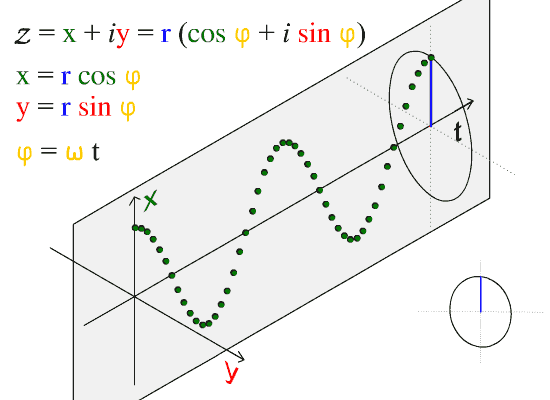
شكل يوضح علاقة الدالة الموجية بالحركة الدائرية. المطال هو أكبر قيمة ل x. تبدأ الموجة هنا عندما تكون x = المطال والزاوية صفر. تمثل الحركة هنا دورتين كاملتين (إثنين من طول الموجة.
نفترض حالة حركة دائرية فتكون السرعة الزاوية’ ، أي معدل تغير الزاوية مع الزمن :

{\displaystyle \omega ={\frac {2\pi }{T}}}\omega ={\frac {2\pi }{T}}
ومنه نحصل على زمن الدورة T الواحدة :

{\displaystyle T={\frac {2\pi }{\omega }}}T={\frac {2\pi }{\omega }}
وتبلغ سرعة نقطة {\displaystyle v}v على دائرة دوران ذات نصف قطر {\displaystyle R}R :

{\displaystyle v=\omega \cdot R={\frac {2\pi R}{T}}.}v=\omega \cdot R={\frac {2\pi R}{T}}.
ويبلغ عدد الدورات في الثانية :

{\displaystyle n={\frac {\omega }{2\pi }}}n={\frac {\omega }{2\pi }}
في الحركة الاهتزازية يمثل التردد {\displaystyle f}f عدد الاهتازات الكاملة (الدورات) في وحدة الزمن. وفي كل دورة يتغير مسقط المطال طبقا لدالة جيبية ويعبر زاوية قدرها {\displaystyle 2\pi }2\pi .

من ذلك يمكننا حساب التردد الزاوي :

{\displaystyle \omega =2\pi \cdot f.}

وتناظر صيغة التردد صيغة عدد الدورات :

{\displaystyle f={\frac {\omega }{2\pi }}.}f={\frac {\omega }{2\pi }}.

هذه المعادلة تبين العلاقة بين التردد f والسرعة الزاوية {\displaystyle \omega .}\omega .. ويقاس التردد هرتز أو 1/ثانية، أما السرعة الزاوية فهي تقاس ب راديان/ثانية.